heute mal ein ganz anderes Thema. Diese coolen Shirts habe ich heute bei www.t4ri.de entdeckt, vielleicht für euch auch interessant


heute mal ein ganz anderes Thema. Diese coolen Shirts habe ich heute bei www.t4ri.de entdeckt, vielleicht für euch auch interessant

Die Spezialistin für die Hochzeitspapeterie Anne Riemer zeigte auf der WeddingNight ihre individuell gestalteten Einladungssets, Tischkarten und Hochzeitskollektionen.

Die Hochzeitsmesse Wedding-Night Herzogenaurach hat 2019 zum ersten Mal die Tore geöffnet und heiratswillige Paare zum Staunen eingeladen. Im Messebereich fanden sich viele Aussteller rund um das Thema Hochzeit und Heiraten in der Region. Insbesondere der Stand von Anne Riemer Design lockte viele Besucher an. Weitere Infos siehe https://www.instagram.com/anneriemer.design und http://anneriemer.de/
Quelle: – A Critical Review of Recurrent Neural Networks for Sequence Learning, Lipton et al. 2015
Unzählige Lernaufgaben erfordern den Umgang mit sequentiellen Daten. Bilderkennung, Sprachsynthese und Musikerzeugung benötigen alle ein Sequenz-Modell. Rekurrente (wiederkehrende) neuronale Netze (RNNs) speichern und lernen die Dynamik von Sequenzen mittels Zyklen in einem Netzwerk von Knoten.
Dieser Abschnitt stellt eine formale Notation vor und beschreibt Neuronale Netze im Allgemeinen.
Die Eingabe zu einem RNN ist eine Sequenz und / oder sein Ergebnis ist eine Sequenz. Eine Eingangs-Sequenz (ein Eingangs-Vektor) kann mit x (1), x (2), …, x (T) bezeichnet werden, wobei jeder Datenpunkt x (t) ein reeller Wert ist. In ähnlicher Weise kann eine Zielsequenz (y (1), y (2),…,y (T)) bezeichnet werden. Ein Trainingssatz ist typischerweise ein Satz von Beispielen, bei denen jedes Beispiel ein (Eingabesequenz, Zielsequenz) Paar ist. Die Eingabe oder die Ausgabe kann auch ein einzelner Datenpunkt sein. Der maximale Zeitindex der Sequenz wird T genannt.
Es werden nachfolgend Hochzeiger mit Klammern für Zeit-Informationen verwendet, um Verwechslungen zwischen Sequenzschritten und Indizes der Knoten zu verhindern. Eine Eingabesequenz besteht somit aus Datenpunkten [latex ]\chi^{(t)}[/latex] die sich als diskrete Sequenz von durch t indizierten Zeitschritten zusammensetzt. Eine Zielsequenz besteht aus Datenpunkten [latex ]y^{(t)}[/latex].
Wenn ein Modell vorhergesagte Datenpunkte erzeugt, werden diese markiert [latex ]\hat{y}^{(t)}[/latex] dargestellt.
Neuronale Netze sind biologisch inspirierte Berechnungsmodelle. Ein neuronales Netzwerk besteht aus einem Satz von künstlichen Neuronen, als Knoten oder Einheiten und eine Reihe von gerichteten Kanten zwischen ihnen, die intuitiv die Synapsen in einem biologischen neuronalen Netzwerk repräsentieren.
Mit jedem verbunden Neuron j ist eine Aktivierungsfunktion [latex ]l_j \bigodot[/latex] verknüpft, die manchmal auch als Link-Funktion bezeichnet wird. Es wird die Notation [latex ]l_j [/latex] und nicht [latex ]h_j [/latex] verwendet, dieses im Gegensatz zu einigen anderen Darstellungen, um die Aktivierungsfunktion aus den Werten der verborgenen Knoten in einem Netzwerk zu unterscheiden (in der Literatur auch allgemein mit h bezeichnet).
Jedem Knoten j‘ bis j ist ein Gewicht [latex ]w_{jj^{\prime}}[/latex] zugeordnet. Gemäß mehreren Grundlagenpapieren [Hochreiter und Schmidhuber, 1997, Gers et al., 2000, Gers, 2001, Sutskever et al., 2011] indexieren wir auch hier Neuronen mit j und j‘ und [latex ]w_{jj^{\prime}}[/latex] das dazu korrespondierende Gewicht, als die gerichtete Verbindung zum Knoten j vom Knoten j‘. Es ist wichtig zu beachten, dass in vielen Referenzen die Indizes getauscht sind, d.h. [latex ]w_{jj^{\prime}}{\neq}w_{j^{\prime}j}[/latex] bezeichnet hier das Gewicht von-bis auf der gerichteten Kante vom Knoten j‘ zum Knoten j, wie in den Unterlagen von Elkan[2015] und in Wikipedia [2015].
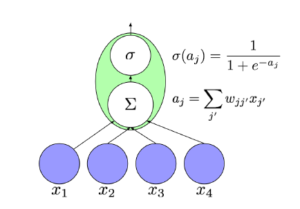
Der Wert [latex ]v_j[/latex] jedes Neurons j wird durch Anwenden seiner Aktivierungsfunktion zu einer gewichteten Summe der Werte seiner Eingangsknoten berechnet:
[latex ]v_j = l_j \left( \sum_{\substack{j^{\prime}}} w_{jj^{\prime}} \cdot v_{j^{\prime}}\right)[/latex]
Zur Vereinfachung nennen wir die gewichtete Summe innerhalb der Klammern als eingehende Aktivierung und bezeichnen dieses auch als [latex ]a_j[/latex]:
[latex ]a_j = \sum_{\substack{j^{\prime}}} w_{jj^{\prime}} \cdot v_{j^{\prime}}[/latex]
In Diagrammen sind Neuronen als Kreise und Übergänge als verbindende Pfeile dargestellt.
Häufige Optionen für die Aktivierungsfunktion ist die Sigmoid-Funktion:
[latex ]\sigma (a_j) = 1/(1 + \mathrm{e}^{-a_j})[/latex]
und die tanh-Funktion:
[latex ]\phi (a_j) = (\mathrm{e}^{a_j} – \mathrm{e}^{-a_j})/(\mathrm{e}^{a_j} + \mathrm{e}^{-a_j})[/latex]
 Die Aktivierungsfunktion an den Ausgangsknoten hängt von der Aufgabe ab. Für Mehr-Klassen-Klassifizierung mit K alternativen Klassen, wenden wir eine Softmax-Nichtlinearität in einer Ausgangsschicht von K Knoten an. Die Softmax-Funktion wird wie folgt berechnet:
Die Aktivierungsfunktion an den Ausgangsknoten hängt von der Aufgabe ab. Für Mehr-Klassen-Klassifizierung mit K alternativen Klassen, wenden wir eine Softmax-Nichtlinearität in einer Ausgangsschicht von K Knoten an. Die Softmax-Funktion wird wie folgt berechnet:
[latex ]\hat y_k = \mathrm{e}^{a_k} / \sum_{\substack{ \\
K \\
k^{\prime}=1
}} \mathrm{e}^{a_{k^{\prime}}}[/latex]
Der Nenner der Softmax-Funktion ist ein Normalisierungsbegriff, der aus der Summe der Zähler besteht, so dass sich die Ausgänge aller Knoten zu eins addieren.
In einem neuronalen Modell muss man die Reihenfolge der Berechnung bestimmen. Sollen nur einzelne Knoten zu einem Zeitpunkt abgetastet und aktualisiert werden, oder sollen die Werte aller Knoten auf einmal berechnet werden und dann alle Aktualisierungen gleichzeitig angewendet werden.
Feedforward-Netzwerke sind eine eingeschränkte Klasse von Netzwerken, die sich mit diesem Problem beschäftigen, indem sie Zyklen verbieten. Angesichts der Abwesenheit von Zyklen können alle Knoten angeordnet werden und die Ausgänge in jeder Schicht können mit den Ausgängen von berechnet Knoten aus unteren Schichten bestimmt werden.
Der Eingang x zu einem Feedforward – Netzwerk ist die unterste Schicht. Jede höhere Schicht wird dann sukzessive bis zur Ausgabe berechnet. An der obersten Schicht wird
[latex ]\hat{y}[/latex] erzeugt. Feedforward-Netzwerke werden häufig für überwachte Lernaufgaben verwendet, wie Klassifikation und Regression. Das Lernen wird durch iteratives Aktualisieren jedes der Gewichte erreicht. Hierbei wird die Differenz minimiert, die den Abstand zwischen dem Ausgangssignal [latex ]\hat{y}[/latex] und dem Ziel y kennzeichnet.
Der erfolgreichste Algorithmus für das Training neuronaler Netze ist die Backpropagation, eingeführt von Rumelhart et al. [1985]. Backpropagation verwendet die Kettenregel. Das Training ist aber nicht einfach, da in einem neuronalen Netzwerk mit sigmoidalen oder tanh – Aktivierungsfunktionen der Knoten in jeder Ebene niemals den Wert Null annehmen können.
Rekurrente Neuronale Netze (RNN) sind Feedforward Neuronale Netze, die durch die Einbeziehung von Übergängen, die aneinander angrenzende Zeitschritte überspannen und einen Zeitablauf einführen. Wie Feedforward-Netzwerke haben RNNs keine Zyklen. Jedoch Übergänge, die angrenzende Zeitschritte verbinden und eine Ablauffolge definieren. Diese können auch Zyklen bilden, einschließlich Zyklen der Länge eins, die Selbstverbindungen durch Anreihung des immer wieder gleichen Knotens sind.
Das Training wiederkehrenden Netzwerken ist lange Zeit als schwierig erachtet worden. Insbsondere Aufgrund der Schwierigkeit des Erlernens von weitreichenden Abhängigkeiten, wie von Bengio et al.[1994] und erweitert von Hochreiter et al. [2001] betrachtet. Die Probleme von verschwindenden und explodierden Gradienten treten auf, wenn die Fehler über viele Zeitschritte übertragen werden. Als kleines Beispiel betrachten wir ein Netzwerk mit einem einzigen Eingangsknoten, einem einzelnen Ausgangsknoten und einem einzigen wiederkehrenden verdeckten Knoten. Man betrachte nun einen Eingang, der zum Zeitpunkt t1 an das Netzwerk übergeben wird, und einen Fehler, der zum Zeitpunkt t2 berechnet wird, wobei die Eingabe von Null in den dazwischenliegenden Zeitschritten vorausgesetzt wird. Das Binden von Gewichten über Zeitschritte bedeutet, dass die wiederkehrenden Übergänge am versteckten Knoten j immer das gleiche Gewicht haben. Daher wird der Beitrag der Eingabe zum Zeitpunkt t zum Ausgang zum Zeitpunkt t1 entweder explosionsartig oder exponentiell schnell null, wenn t2-t1 groß wird. Daher wird die Ableitung des Fehlers in Bezug auf die Eingabe entweder explodieren oder verschwinden.
Welche der beiden Phänomene auftritt hängt davon ab, ob das Gewicht der rekurrierenden Übergänge [latex ]w_{jj} > 1[/latex] oder [latex ]w_{jj} < 1[/latex] und wie die Aktivierungsfunktion im verborgenen Knoten ausgelegt ist. Bei einer sigmoidalen Aktivierungsfunktion ist das Problem des Verschwindens des Gradienten stärker, aber mit einer gleichgerichteten Lineareinheit max(0; x) ist es einfacher, den explodierenden Gradienten vorzustellen. Pascanu et al. [2012] gibt eine gründliche mathematische Behandlung der verschwindenden und explodierenden Gradientenprobleme, die die genauen Bedingungen charakterisieren, unter denen diese Probleme auftreten können. Angesichts dieser Bedingungen schlagen sie einen Ansatz zur Ausbildung über einen Regularisierungsausdruck vor, der die Gewichte zu Werten zwingt, bei denen der Gradient weder verschwindet noch explodiert.
Truncated backpropagation through time (TBPTT) ist eine Lösung für das explodierende Gradientenproblem für kontinuierlich laufende Netzwerke [Williams und Zipser, 1989]. Bei TBPTT wird eine maximale Anzahl von Zeitschritten festgelegt, entlang derer Fehler übertragen werden dürfen. Während TBPTT mit einem kleinen Cutoff verwendet werden kann, um das explodierende Gradientenproblem zu lindern, erfordert es das Opfer der Fähigkeit Long-Range-Abhängigkeiten lernen zu können. Die später beschriebene LSTM-Architektur verwendet sorgfältig konstruierte Knoten mit wiederkehrenden Kanten mit festem Einheitsgewicht als Lösung für das Problem des Verschwindens des Gradienten.
Die Grundlagenforschung über RNN Netzwerke fand in den 1980er Jahren statt. In 1982 führte Hopfeld eine Familie RNN Netze ein. Sie wurden durch Gewichte zwischen den Knoten und Verknüpfungsfunktionen mit einfachen Schwellenwerten definiert. Diese Hopfeld-Netzwerke sind nützlich für das Wiedererkennen eines gespeicherten Musters und sind die Vorläufer von Auto-Encodern.
Die Architektur von Elman [1990] verwendet zusätzlich verdeckte Knoten. Die
Architektur entspricht einem einfachen RNN, in dem jedem verdeckten Knoten eine einzelne selbst verbundene wiederkehrende Kante ist. Die Idee der gewichteten wiederkehrenden Kanten, bei denen versteckte Knoten verbunden sind, war in der Arbeit
LSTM-Netzwerke [Hochreiter und Schmidhuber, 1997] dann grundlegend für weitere Verbesserungen.
Das Lernen mit RNN Netzwerken war anfangs schwierig. Die erfolgreichsten RNN-Architekturen für das Sequenzlernen stammen aus zwei Beiträgen Veröffentlicht im Jahr 1997. Die erste Papier, Long Short-Term Memory von Hochreiter und Schmidhuber [1997], setzt eine Speicherzelle vor die traditionellen Knoten in der verborgenen Schicht eines Netzwerks. Mit diesen Gedächtniszellen sind die Netzwerke in der Lage die Lernschwierigkeiten zu überwinden.
Das zweite Papier, Bidirektionale RNN (BRNN) von Schuster und Paliwal [1997], führt eine Architektur ein, in der Informationen aus der Zukunft und der Vergangenheit verwendet werden, um die Ausgabe an jedem Punkt in der Sequenz zu bestimmen. Dies steht im Gegensatz zu bisherigen Netzen, in denen nur die vergangene Eingabe die Ausgabe beeinflussen kann.
Im nächsten Abschnitt erläutern wir die LSTM und BRNN und beschreiben die neuronale Turingmaschine (NTM), die RNNs mit einem adressierbaren externen Speicher erweitert [Graves et al., 2014].
 LSTM-Modelle helfen in erster Linie, das Problem das Verschwinden von Gradienten zu überwinden. Dieses Modell ähnelt einem herkömmlichen, wiederkehrenden neuronalen Netz mit einer verborgenen Schicht, wobei jedoch jeder gewöhnliche Knoten in der verborgenen Schicht durch eine Speicherzelle ersetzt wird.
LSTM-Modelle helfen in erster Linie, das Problem das Verschwinden von Gradienten zu überwinden. Dieses Modell ähnelt einem herkömmlichen, wiederkehrenden neuronalen Netz mit einer verborgenen Schicht, wobei jedoch jeder gewöhnliche Knoten in der verborgenen Schicht durch eine Speicherzelle ersetzt wird.
Jede Speicherzelle enthält einen Knoten mit einer selbstverbundenen wiederkehrenden Kante von festem Gewicht 1, wodurch sichergestellt wird, dass der Gradient über viele Zeitschritte hinweggehen kann, ohne verschwinden oder explodieren zu müssen. Um Referenzen auf eine Speicherzelle und nicht auf einen gewöhnlichen Knoten zu unterscheiden, benutzen wir den Index c.
Der Begriff LSTM „langes Kurzzeitgedächtnis“ kommt aus der Intuition, dass
einfache wiederkehrende neuronale Netze ein Langzeitgedächtnis in Form von Gewichten haben. Die Gewichte ändern sich während des Trainings langsam und verschlüsseln das allgemeine Wissen über die Daten. Sie haben auch Kurzzeitgedächtnis in Form von kurzlebigen Aktivierungen, die von jedem Knoten zu aufeinanderfolgenden Knoten übergehen. Das LSTM-Modell führt einen Zwischenspeichertyp über die Speicherzelle ein. Eine Speicherzelle ist eine zusammengesetzte Einheit, die aus einfacheren Knoten in einem spezifischen Konnektivitätsmuster aufgebaut ist, die in Diagrammen durch den Buchstaben [latex ]\Pi[/latex] dargestellt sind. Nachstehend werden alle Elemente der LSTM-Zelle aufgezählt und beschrieben.
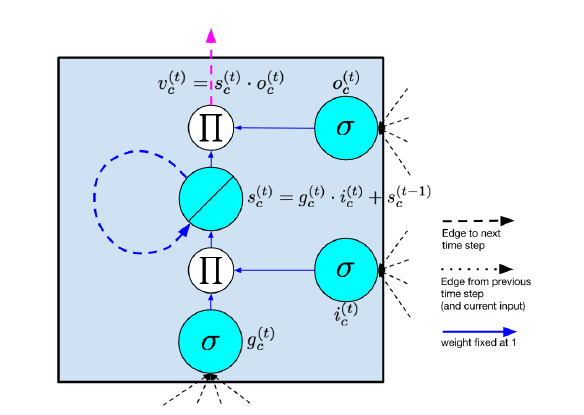
Die nachfolgende Vektor-Notation bezieht sich auf die Werte der Knoten in einer ganzen Schicht von Zellen. Beispielsweise ist s ein Vektor, der den Wert von [latex ]s_c [/latex] an jeder Speicherzelle c in einer Schicht enthält. Der Index c indiziert eine einzelne Speicherzelle. Ein LSTM-Block besteht aus:
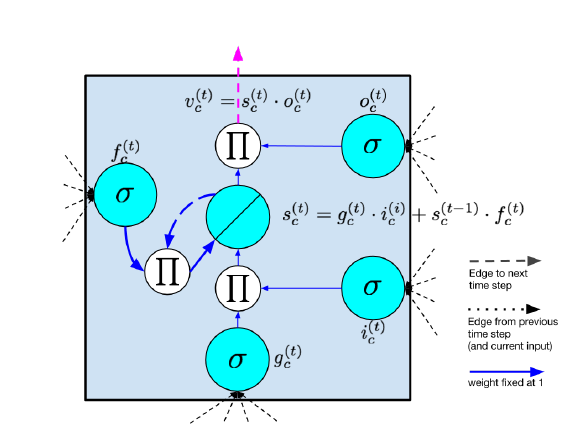
Als das ursprüngliche LSTM eingeführt wurde, wurden verschiedene Variationen vorgeschlagen. Die Löschknoten wurden im Jahr 2000 vorgeschlagen und waren nicht Teil des ursprünglichen LSTM-Design. Sie haben sich jedoch bewährt und sind in den meisten modernen Implementierungen Standard. Im selben Jahr haben Gers und Schmidhuber [2000] Gucklochverbindungen vorgeschlagen, die vom internen Zustand direkt zu den Eingangs- und Ausgangsknoten desselben Knotens übergehen, ohne vorher vom Ausgangsknoten moduliert werden zu müssen. Sie berichten, dass diese Verbindungen die Leistung bei Timing-Aufgaben verbessern, in denen das Netzwerk lernen muss, präzise Intervalle zwischen Ereignissen zu messen. Die Intuition der Guckloch-Verbindung kann durch folgendes Beispiel erfasst werden. Betrachten Sie ein Netzwerk, das lernen muss, Objekte zu zählen und eine gewünschte Ausgabe zu erzeugen, wenn n Objekte gesehen worden sind. Das Netzwerk könnte lernen, einige feste Menge an Aktivierung in den internen Zustand zu lassen, nachdem die Objekte registriert wurden. Diese Aktivierung wird im internen Zustand [latex ]s_c [/latex] durch das konstante Fehlerkarussell eingefangen und iterativ jedes Mal inkrementiert, wenn ein anderes Objekt gesehen wird. Wenn das n-te Objekt sichtbar ist, muss das Netzwerk Inhalte aus dem internen Zustand [latex ]s_c [/latex] auswerten, so dass es die Ausgabe beeinflussen kann. Um dies zu erreichen, muß das Ausgangsknoten [latex ]o_c [/latex] den Inhalt des internen Zustands [latex ]s_c [/latex] kennen. Somit sollte [latex ]s_c [/latex] eine Eingabe für [latex ]o_c [/latex] haben.
Die Berechnung im LSTM-Modell erfolgt gemäß den folgenden Gleichungen, die bei jedem Schritt durchgeführt werden. Diese Gleichungen benennen den vollständigen Algorithmus für ein modernes LSTM mit Löschknoten:
Eingangsknoten: [latex ]g^{(t)} = \phi \left(W^{gx} \chi^{(t)} + W^{gh} h^{(t-1)} + b_g \right) [/latex]
Gate-Eingangsknoten: [latex ]i^{(t)} = \sigma \left(W^{ix} \chi^{(t)} + W^{ih} h^{(t-1)} + b_i \right) [/latex]
Löschknoten: [latex ]f^{(t)} = \sigma \left(W^{fx} \chi^{(t)} + W^{fh} h^{(t-1)} + b_f \right) [/latex]
Gate-Ausgangsknoten: [latex ]o^{(t)} = \sigma \left(W^{ox} \chi^{(t)} + W^{oh} h^{(t-1)} + b_o \right) [/latex]
Interner Zustand: [latex ]s^{(t)} = g^{(t)} \odot i^{(t)} + f^{(t)} \odot s^{(t-1)} [/latex]
Verdeckter Zustand: [latex ]h^{(t)} = \phi \left(s^{(t)}\right) \odot o^{(t)} [/latex]
Ausgangsknoten: [latex ]v^{(t)} = s^{(t)} \odot o^{(t)} [/latex]
Hierbei gehen in die Berechnung die zur Zeit t empfangene Knoten vom aktuellen Datenpunkt [latex ]\chi^{(t)}[/latex] und auch verdeckte Knotenwerte [latex ]h^{(t-1)}[/latex] im vorherigen Zustand, d.h. zum Zeitpunkt t-1 des Netzwerks ein. Der aktuelle verdeckte Zustand ist mit [latex ]h^{(t)}[/latex] definiert.
Ergänzend sind [latex ]W^{gx}, W^{ix}, W^{fx}, W^{ox}[/latex] die Matrizen der konventionellen Gewichte zwischen den Eingangswerten und den Gates und [latex ]W^{gh}, W^{ih}, W^{fh}, W^{oh}[/latex] die Matrizen der Gewichte zwischen der verborgenen Schicht des Gates und verborgenen Knoten im zurückliegenden Zeitschritt. Die Vektorn [latex ]b_g, b_i, b_f, b_o[/latex] sind Biasparameter, die es ermöglichen einen Offset zu lernen.
Diese Gleichungen schließen Löschknoten mit ein, aber nicht die Gucklochverbindungen. Die Berechnungen für das einfachere LSTM ohne Löschknoten werden durch Einstellen von [latex ]f ^{(t)} = 1[/latex] für alle t erhalten. Es wird die tanh-Funktion [latex ]\phi[/latex] für den Eingangsknoten g nach dem Stand der Technik von Zaremba und Sutskever [2014] verwendet. Im ursprünglichen LSTM-Papier ist jedoch die Aktivierungsfunktion für g die Sigmoide [latex ]\sigma[/latex]
Intuitiv kann der LSTM-Block im Hinblick auf den Forward-Pass lernen, wann es in den internen Zustand gehen soll. Solange der Ausgangs-Gateknoten den Wert Null annimmt, kann keine Aktivierung eingegangen werden. Wenn beide Gateknoten geschlossen sind, wird die Aktivierung in der Speicherzelle eingeschlossen, weder wachsend noch schrumpfend, noch beeinflusst der Block den Ausgang bei Zwischenzeitschritten. Im Hinblick auf den Rückwärtslauf ermöglicht dieses, dass sich der Gradient über viele Zeitschritte verändert und weder explodiert noch verschwindet. In der Praxis hat das LSTM eine überlegene Fähigkeit gezeigt, langzeitige Abhängigkeiten zu erlernen. Demzufolge wird in der Mehrzahl heute das LSTM-Modell verwendet.
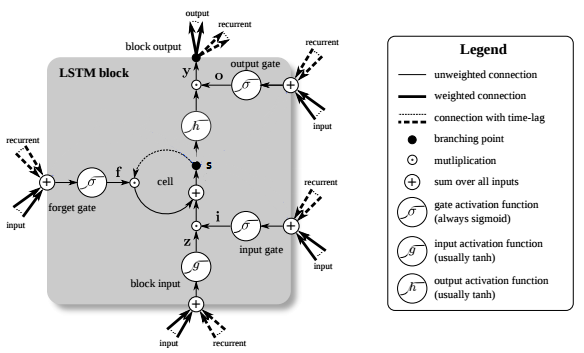 Dieses weitere Übersichtsbild zeigt noch anschaulicher den verdeckten Knoten h. Es ist ebenfalls dargestellt, dass die Speicherzellen des LSTM-Block in der Transformation des Eingangs die unterschiedlichen Funktionen zur Addition und Multiplikation bieten. In diesem Bild hat der Ausgangsknoten die Bezeichnung y, oben wurde v verwendet. Das zentrale Pluszeichen ist im Wesentlichen das Geheimnis des LSTMs. Statt den nachfolgenden Zellzustand durch Multiplikation seines aktuellen Zustands mit neuem Eingang zu bestimmen, addieren sich die beiden und das macht die Besonderheit aus.
Dieses weitere Übersichtsbild zeigt noch anschaulicher den verdeckten Knoten h. Es ist ebenfalls dargestellt, dass die Speicherzellen des LSTM-Block in der Transformation des Eingangs die unterschiedlichen Funktionen zur Addition und Multiplikation bieten. In diesem Bild hat der Ausgangsknoten die Bezeichnung y, oben wurde v verwendet. Das zentrale Pluszeichen ist im Wesentlichen das Geheimnis des LSTMs. Statt den nachfolgenden Zellzustand durch Multiplikation seines aktuellen Zustands mit neuem Eingang zu bestimmen, addieren sich die beiden und das macht die Besonderheit aus.
Zusammen mit dem LSTM ist eine der am häufigsten verwendeten RNN-Architekturen das bidirektionale Neuronennetzwerk (BRNN), das zuerst von Schuster und Paliwal [1997] beschrieben wurde.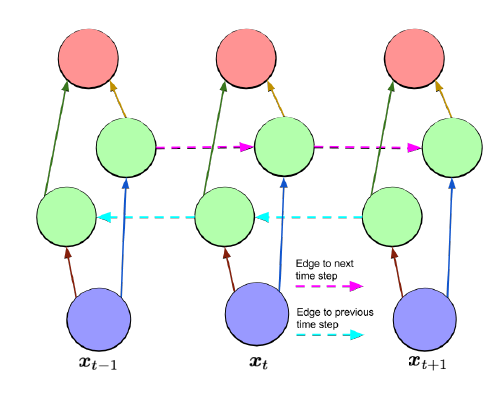
In dieser Architektur gibt es zwei Schichten von versteckten Knoten. Beide versteckten Schichten sind mit Eingang und Ausgang verbunden. Die beiden verborgenen Schichten unterscheiden sich dadurch, dass die erste wiederkehrende Verbindungen auf den letzten Zeitschritten weist, während in der zweiten die Richtung der wiederkehrenden Verbindungen auf den nächsten Schritt zeigt. Die Aktivierung erfolgt rückwärts entlang der Folge. Bei einer Eingangssequenz und einer Zielsequenz kann das BRNN durch eine normale Backpropagation nach dem Entfalten über die Zeit trainiert werden. Die folgenden drei Gleichungen beschreiben ergänzend einen BRNN:
Verdeckter Zustand Vorwärts: [latex ]h^{(t)} = \sigma \left(W^{hx} \chi^{(t)} + W^{hh} h^{(t-1)} + b_h\right) [/latex]
Verdeckter Zustand Rückwärts: [latex ]h^{(t)} = \sigma \left(W^{zx} \chi^{(t)} + W^{zz} h^{(t-1)} + b_z\right) [/latex]
Ausgabeknoten: [latex ]\hat y^{(t)} = softmax\left(W^{yh} h^{(t)} + W^{yz} z^{(t)} + b_y\right) [/latex]
Eine Begrenzung des BRNN ist, dass er nicht kontinuierlich laufen kann, da er einen festen Endpunkt in der Zukunft und in der Vergangenheit erfordert. Ferner ist er kein geeigneter Maschinellen Lernalgorithmus für die Online-Anwendung, da es nicht plausibel ist, Informationen aus der Zukunft zu empfangen, d.h. vorab Sequenzelemente zu kennen, die noch nicht beobachtet wurden. Aber für die Vorhersage über eine zukünftig mögliche Folge ist es oft sinnvoll, sowohl Vergangenheit als auch zukünftige Sequenzelemente zu berücksichtigen. Deshalb findet er insbesondere zur Auswertung natürlicher Sprache eine Anwendung, wenn noch nicht ausgesprochene Sätze vorab betrachtet werden sollen.
Die LSTM und BRNN sind in der Tat kompatible Ideen. Das erstere führt eine neue Grundeinheit ein, aus der eine verborgene Schicht zu bilden ist, während die letztere die Verdrahtung der verborgenen Schichten betrifft, unabhängig davon, welche Knoten sie enthalten. Ein derartiger Ansatz, der als BLSTM bezeichnet wird, wurde verwendet, um Stand der Technik auf Handschrifterkennung und Phonemklassifikation zu erreichen [Graves and Schmidhuber, 2005, Graves et al., 2009].
Die neuronale Turingmaschine (NTM) erweitert rekurrierende neuronale Netze mit einem adressierbaren externen Speicher [Graves et al., 2014]. Diese Arbeit verbessert die Fähigkeit von RNNs, komplexe algorithmische Aufgaben wie das Sortieren durchzuführen. Die Autoren nehmen Anregungen aus Theorien der Kognitionswissenschaft, die darauf hindeuten, dass die Menschen eine „zentrale Exekutive“ besitzen, die mit einem Gedächtnispuffer interagiert [Baddeley et al., 1996]. In Analogie zu einer Turingmaschine, bei der ein Programm Leseköpfe und Schreibköpfe lenkt, um mit einem externen Speicher in Form eines Bandes zu interagieren, wird das Modell als Neural-Turingmaschine bezeichnet.
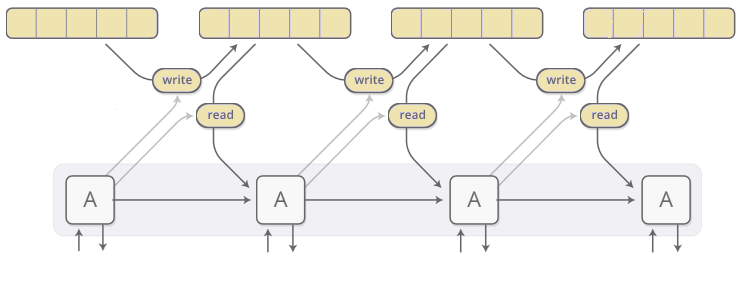 NTM können den Ort, an dem sie lesen oder schreiben, differenzierbar machen und sie können lernen, wo sie lesen und schreiben sollen. NTMs adressieren dabei in einem neuen Speicherverfahren: In jedem Schritt lesen und schreiben sie in allen Zellen in unterschiedlichem Umfang.
NTM können den Ort, an dem sie lesen oder schreiben, differenzierbar machen und sie können lernen, wo sie lesen und schreiben sollen. NTMs adressieren dabei in einem neuen Speicherverfahren: In jedem Schritt lesen und schreiben sie in allen Zellen in unterschiedlichem Umfang.
Die beiden Hauptkomponenten eines NTM sind eine Controller- und Memory-Matrix. Der Controller, der ein wiederkehrendes oder vorwärts gerichtetes neuronales Netzwerk sein kann, verarbeitet Eingang und Ausgang zur Außenwelt, sowie die Übergabe von Schreib- und Lesen-Befehlen an den Speicher. Der Speicher wird durch eine große Matrix von N Speicherplätzen repräsentiert, von denen jeder ein Vektor der Dimension M ist. Zusätzlich erleichtert eine Anzahl von Lese- und Schreibköpfen die Interaktion zwischen dem Controller und der Speichermatrix. Trotz dieser zusätzlichen Fähigkeiten ist das NTM differenzierbar von Ende zu Ende und kann durch Varianten der stochastischen Gradientenabsenkung mit BPTT trainiert werden.
Graves et al. [2014] wählen algorithmische Aufgaben aus, um die Leistung des NTM-Modells zu testen. Unter Algorithmik verstehen wir, dass für jede Aufgabe die Zielausgabe für eine gegebene Eingabe nach einem einfachen Programm berechnet werden kann, wie es leicht in einer beliebigen universellen Programmiersprache implementiert werden kann. Ein Beispiel ist die Kopieraufgabe, wobei die Eingabe eine Folge binärer Binärvektorknoten mit fester Länge ist, gefolgt von einem Delimitersymbol. Die Ziel-Ausgabe ist eine Kopie der Eingabesequenz.
Bei einer anderen Task-Priority-Sortierung besteht eine Eingabe aus einer Sequenz von binären Vektoren zusammen mit einem bestimmten skalaren Prioritätswert für jeden Vektor. Die Ziel-Ausgabe ist die Folge von Vektoren, sortiert nach Priorität.
Die Experimente testen, ob ein NTM durch beaufsichtigtes Lernen trainiert werden kann, um diese gemeinsamen Algorithmen korrekt und effizient umzusetzen. Interessanterweise verallgemeinern sich die auf diese Weise gefundenen Lösungen einigermaßen gut zu den Eingängen, die länger sind als die im Trainingsset dargestellten. Im Gegensatz dazu verläuft das LSTM ohne externen Speicher nicht gut zu längeren Eingängen. Die Autoren vergleichen drei verschiedene Architekturen, nämlich ein LSTM RNN, ein NTM mit einem Feedforward Controller und ein NTM mit einem LSTM Controller. Bei jeder Aufgabe übertreffen beide NTM-Architekturen den LSTM RNN signifikant sowohl in der Trainingsmenge als auch in der Generalisierung auf Testdaten.
Weitere Details und Betrachtungen zu NTM folgen in einem nachfolgenden Artikel.